消失的除法指令：Part1

之前学汇编的时候观察到一个现象，我在 C 语言中写了一个函数进行除法操作，但是编译得到的汇编代码中却没有除法指令，取而代之的是一条乘法指令。

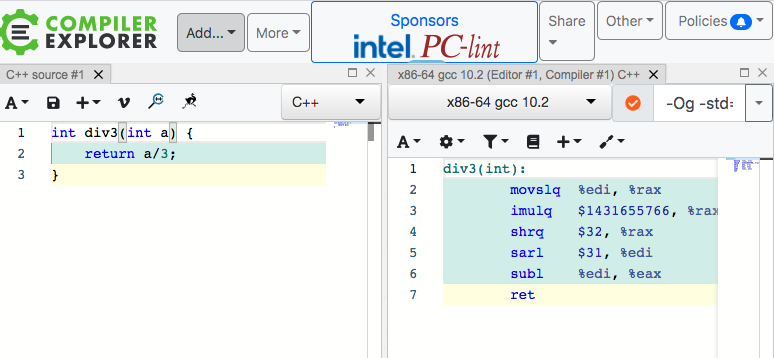
图片对应的 GodBolt 地址在这里，可以看到有一个 imulq 指令，这是一个乘法指令，乘了一个奇怪的数字 1431655766。

为什么编译器要这样操作？为什么能这样操作？1431655766 这个数字又是怎么来的？

Assembly Code

我们先来分析一下 GodBolt 中的汇编代码，注意这里使用的编译器是 GCC 10。

div3(int):
  movslq  %edi, %rax
  imulq   $1431655766, %rax, %rax
  shrq    $32, %rax
  sarl    $31, %edi
  subl    %edi, %eax
  ret

一共 6 条指令，除去最后一条 ret 指令用于函数返回，总计 5 条指令解决了除以三运算。

💡TIP:

关于 X86/X64 的汇编，Intel 的官方手册 Intel® 64 and IA-32 Architectures Software Developer’s Manuals 是居家旅行必备的。

GCC 使用的是 AT&T 汇编语法，基本特点是 source 在左边，target 在右边。

首先，movslq %edi, %rax 将 edi 寄存器中的值有符号扩展为 64bit 然后移动到 rax 寄存器中。

MOVSLQ is move and sign-extend a value from a 32-bit source to a 64-bit destination.

我们的函数接收 32-bit 的有符号整数作为第一个参数，可以看到背后的 ABI 规范是第一个参数存储在 edi 寄存器中。

💡TIP:

这里使用的 ABI 叫做 AMD64 ABI，我没有找到特别正式的资料，但是在这个页面找到了传参的相关说明。

The basic function calling convention is different for the AMD ABI. Arguments are placed in registers. For simple integer arguments, the first arguments are placed in the %rdi, %rsi, %rdx, %rcx, %r8, and %r9 registers, in that order.

接下来的 imulq $1431655766, %rax, %rax 就比较简单了，将 rax 中的数字和 1431655766 乘在一起，结果存储在 rax 中。

我们知道 rax 存储的的数字是 edi 扩展来的，所以是 32-bit 范围内的有符号整数。1431655766 也是 32-bit 范围内的有符号整数，两个 32bit 的整数相乘，结果不会超过 64bit，所以这一步运算不会溢出。

shrq $32, %rax 将 rax 寄存器中的值逻辑右移 32 位，也就是 rax 中的高 32 位到了低位，高位全部变成了 0。

sarl $31, %edi 这里的 a 是 arithmetic 算术的意思，所以这是是将 edi 寄存器算术右移 31 位，也就是此时最高位到了最低位，根据 edi 中数字的正负，结果的二进制要么是全 0 要么是全 1，也就是十进制的 0 和 -1。

最后 subl %edi, %eax 将 eax - edi 的值赋给 eax，edi 要么是 0（如果参数 >= 0），要么是 -1（如果参数 < 0）。

所以，我们可以总结一下这里的算法，当我们对一个 32bit 有符号整数 N 除以 3 时，可以等价于

R = N * 1431655766 的高 32 位
如果 N < 0，那么 R = R + 1
返回 R

Validate

我们先抛开数学证明，写个程序验证一下上面的算法确实是正确的。

#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>

#define i32 int32_t
#define i64 int64_t

i32
div3(i32 v)
{
  i32 magic = 1431655766;
  i32 result = ((i64)v * (i64)magic) >> 32;

  if(v < 0) {
    result += 1;
  }

  return result;
}

int
main(void)
{
  srand(0x1234);

  for(int i = 0; i < 10000; i++) {
    i32 v = (i32)rand() * (rand() % 2 == 0 ? 1 : -1);

    i32 got = div3(v);
    i32 expected = v / 3;

    if(got != expected) {
      printf("div3 error! dividend %d, got %d, expected %d\n",
        v,
        got,
        expected);
    }
  }
}

这里我们使用 10000 个随机数进行验证，会发现程序运行正常，没有报错。

Proof

接下来我们在数学上进行证明。

我们先来理清除法这个运算。

在数学中，整数除法得到的是一个有理数。

但是在计算机中，整数除法运算返回的结果是整数，这里面实际上可以有三种模式。

truncating，运算结果始终向 0 截断
floor，运算结果始终向下截断
modulus，余数始终为非负

不管是哪种模式，对于计算机中的除法运算，被除数一定等于商乘以除数加上余数。

这三种模式不存在对错，只是不同的选择，大部分的程序语言和指令集选择的都是 truncating 模式，C 语言也不例外。

所以，计算机中的除法（truncating 模式）和数学中的除法之间的关系可以表达为

接下来我们从数学上证明，上述的乘法算法给出的是正确的除法结果。

首先，我们将 1431655766 这个 Magic Number 改写一下形式。

💡TIP:

关于 Magic Number（魔数），我印象最深的是 Quake III（雷神之锤三）中的 0X5F3759DF。

在一个求平方根倒数的函数中，John Carmack 使用了这个魔数使得计算效率比普通的 1.0f / sqrt(x) 快了 4 倍。

float
InvSqrt(float x)
{
  float xhalf = 0.5f * x;
  int i = *(int *)&x;
  i = 0x5f3759df - (i >> 1); // what the fuck???
  x = *(float *)&i;
  x = x * (1.5f - xhalf * x * x);
  return x;
}

关于约翰卡马克和 ID Software 的传奇故事，有一本书推荐给大家：Master of Doom。

对于 n >= 0，上述运算可以表示为

这里我们使用了一个事实：对有符号整数 n 右移 x 位，相当于对 n/(2^x) 进行 floor 操作。

例如，5 右移 1 位得到 2，是 (5/2 = 2.5) floor 的结果。

-5 右移 1 位得到 -3，是 (-5/2 = -2.5) floor 的结果。

所以，我们现在要做的就是证明如下数学等式成立

我们首先来引入几个定理供后面使用。

THEOREM D0.

THEOREM D1.

THEOREM D2.

这一步的证明相对比较简单。

因 为 所 以 根 据 ， 我 们 得 到

接下来我们来看 n < 0 的情况，此时我们要证明的是

首先把 1 放进 Floor 运算符里面。

根 据 根 据

接下来就比较简单了。

因 为 所 以 根 据 ， 我 们 得 到

Why

最后，我们来看一下，为什么？

为什么编译器要用这样一个算法来计算除以 3 运算？

为什么不直接调用 CPU 的除法指令？

这个问题的答案很好猜测，在保证结果不变的情况下编译器修改了实现细节，那么一定是因为性能。

在我做 HandmadeHero 项目的过程中，不止一次听到 Casey 说过除法的性能非常非常糟糕。

或者准确点来说，在早期计算机中，除法的性能非常非常糟糕，比乘法要慢的多得多，游戏开发者一般会想尽办法避免除法。

Casey 的代码中就充满了规避除法养成的一些习惯。

比如，要把 RGB 值从 0 ~ 255 规整到 0 ~ 1，一般我们的写法是

v3
RGBToLinear(i8 r, i8 g, i8 b) {
  return V3((f32)r / 255.0f, (f32)g / 255.0f, (f32)b / 255.0f);
}

但是，Casey 的代码写法是

v3
RGBToLinear(i8 r, i8 g, i8 b) {
  f32 inv = 1.0f / 255.0f;
  return V3((f32)r * inv, (f32)g * inv, (f32)b * inv);
}

这样写的好处就是只做一次除法，剩下的都是乘法运算。

💡TIP:

注意这里我们举的例子是浮点数除法而不是整数除法。

但是它们背后的机理是一样的，不管是浮点数还是整数，除法运算都比乘法运算要慢。

我很好奇在当代的 CPU 上，除法到底比乘法慢多少？

我们来写个程序比较一下。

在 X86 中，进行除法运算的指令是 idiv。

IDIV r/m32, Signed divide EDX:EAX by r/m32, with result stored in EAX ← Quotient, EDX ← Remainder.

根据手册，idiv x 会将 EDX:EAX 构成的 64bit 整数除以 x 寄存器中的值，商存储在 EAX 中，余数存储在 EDX 中。

我们先把两个算法用汇编写出来，这里我们用的是 nasm，注意它的语法是 Intel，和 GCC 的 AT&T 不一样，target 在左边，source 在右边。

; div.asm
section .text

global div3
global div3ByMul

div3:
  mov eax, edi
  movsx rdx, edi
  shr rdx, 32
  mov ecx, 3
  idiv ecx
  ret

div3ByMul:
  movsx  rax, edi
  imul   rax, 1431655766
  shr    rax, 32
  sar    edi, 31
  sub    eax, edi
  ret

在 Linux 上使用 nasm -f elf64 div.asm 编译得到 div.o 文件。

然后是写一段 C 程序调用上面的两个汇编函数并分别测量时间。

// compare.c
#include <stdint.h>
#include <stdio.h>
#include <sys/time.h>
#include <stdlib.h>

#define i32 int32_t
#define i64 int64_t

i32 div3(i32);
i32 div3ByMul(i32);

long
getUS(struct timeval start)
{
  struct timeval stop;
  gettimeofday(&stop, NULL);

  return (stop.tv_sec - start.tv_sec) * 1000000 + stop.tv_usec - start.tv_usec;
}

int
main(void)
{
  srand(0x1234);

  int n = 100000;

  i32 *randoms = (i32 *)malloc(sizeof(i32) * n);
  if(randoms == NULL) {
    printf("malloc error");
    exit(1);
  }

  struct timeval start;

  while(1) {
    for(int i = 0; i < n; i++) {
      i32 v = (i32)rand() * (rand() % 2 == 0 ? 1 : -1);
      randoms[i] = v;

      // check correctness
      i32 expected = v / 3;

      i32 r1 = div3(v);
      if(r1 != expected) {
        printf("div3 produced error result, got %d, expect %d\n", r1, expected);
      }

      i32 r2 = div3ByMul(v);
      if(r2 != expected) {
        printf("div3ByMul produced error result, got %d, expect %d\n",
          r2,
          expected);
      }
    }

    long t1 = 0;
    long t2 = 0;

    for(int i = 0; i < n; i++) {
      i32 v = randoms[i];

      gettimeofday(&start, NULL);
      div3ByMul(v);
      t1 += getUS(start);
    }

    for(int i = 0; i < n; i++) {
      i32 v = randoms[i];

      gettimeofday(&start, NULL);
      div3(v);
      t2 += getUS(start);
    }

    printf("div3ByMul: %ld \t div3: %ld\n", t1, t2);
  }
}

C 代码很简单，生成一些随机数，首先验证我们的汇编函数返回的结果是正确的，然后测量时间。

gcc -Og compare.c div.o -o compare 编译运行。

在我的 64bit CentOS7 中结果如下：

div3ByMul: 39976   div3: 42402
div3ByMul: 39374   div3: 40548
div3ByMul: 39185   div3: 39914
div3ByMul: 39655   div3: 40626
div3ByMul: 42580   div3: 39658
div3ByMul: 39625   div3: 41399
div3ByMul: 39196   div3: 40411
div3ByMul: 39880   div3: 40563
div3ByMul: 39922   div3: 41022
div3ByMul: 40601   div3: 40245
div3ByMul: 40007   div3: 39863
div3ByMul: 39973   div3: 40509
div3ByMul: 40600   div3: 40302
div3ByMul: 40413   div3: 40462
div3ByMul: 40315   div3: 40448
div3ByMul: 39506   div3: 40808
div3ByMul: 40634   div3: 40772
div3ByMul: 39944   div3: 39894
div3ByMul: 39727   div3: 40631
div3ByMul: 40553   div3: 40393
div3ByMul: 39891   div3: 41112
div3ByMul: 39334   div3: 48546

好像性能差不多？？？

未完待续。

消失的除法指令：Part1

Assembly Code

Validate

Proof

Why

热重载 C

安全背后: 浏览器是如何校验证书的